Samir Brahim Belhaouari

Abstract. This thesis explores the advancements in the Random Jungle algorithm through the introduction of new techniques to Random Forests. It starts with feature engineering on multiple datasets, creating new features that show underlying patterns and relationships within the data. Multiple decision trees are then trained on the extracted features and by utilising a new voting mechanism called “Smart Voting”, we can improve the decision-making process of those trees by considering multiple factors and using different strategies, surpassing the majority vote method normally used in Random Forests. The study evaluates the efficacy of the Random Jungle algorithm in classification by comparing its performance with known and new classifiers, hoping to develop a stronger strategy that improves known classification strategies.

This thesis makes a significant contribution to the field of machine learning by utilizing modern approaches. The insights it offers may be used to a variety of applications that need high-precision categorization. The results could have an impact on enhancing decision-making procedures and the accuracy of applications.

Test Strategies

\(trainingsum=training_{add}+training_{sub}+training_{mul}\)
\(f1sum=f1_{add}+f1_{sub}+f1_{mul}\)
\(puritysum=purity_{add}+purity_{sub}+purity_{mul}\)
Strategy 1:
\(\frac{\sum_{i \in \{add, sub, mul\}}(weight_i\times prob_i)}{weight_{add}+weight_{sub}+weight_{mul}}\)
Strategy 2:
\(\frac{\sum_{i \in \{add, sub, mul\}}(precision_i+recall_i+f1_i)\times prob_i}{\sum_{i \in \{add, sub, mul\}}precision_i+recall_i+f1_i}\)
Strategy 3:
\(\sum_{i \in \{add, sub, mul\}}(\frac{training_i}{trainingsum}\times prob_i)\)
Strategy 4:
\(\frac{\sum_{i \in \{add, sub, mul\}}(weight_i\times prob_i)+(f1\times prob_i)}{\sum_{i \in \{add, sub, mul\}}weight_{i}+f1_{i}}\)
Strategy 5:
\(\sum_{i \in \{add, sub, mul\}}(\frac{training_{i}}{trainingsum}+\frac{f1_{i}}{f1sum}+\frac{purity_{i}}{puritysum})\times prob_i\)

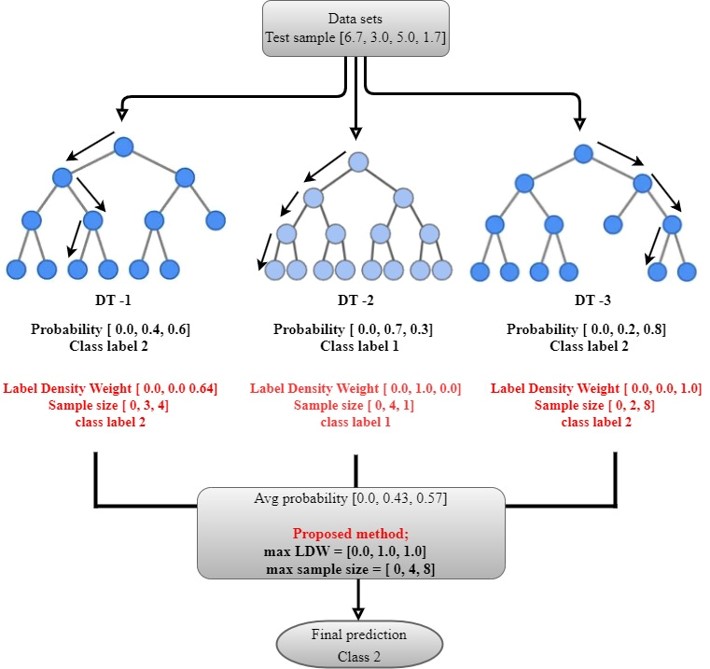
Illustration of the proposed experimental design.