Samir Brahim Belhaouari

Abstract. The Multi-Cluster Jumping Particle Swarm Optimization (MCJPSO) algorithm significantly improves convergence speed and global search efficiency in high-dimensional optimization problems. The algorithm partitions the particle swarm into clusters, each maintaining its own cluster best position \(c_i(t)\), and introduces a jumping strategy to escape local minima. Particle velocities are updated as \(v_i(t+1) = \omega v_i(t) + c_1 \text{rand}(p_i(t)\) \(- x_i(t)) + c_2 \text{rand}(g(t) - x_i(t)) + c_3 \text{rand}(c_i(t) - x_i(t)) + J_i(C_J)\), where the jump function \(J_i(C_J) =\) \(\log \left( \frac{C_J}{0.1 \cdot \text{acceptance}} \right)^\alpha \left( \frac{C_J}{0.1 \cdot \text{acceptance}} + 1 \right)^{-1} + \epsilon \text{rand}_N\) ensures dynamic relocation when stagnation is detected. Semi-random initialization distributes particles across the search space, maximizing exploration. Benchmark tests on twelve functions confirm MCJPSO’s superior performance in convergence speed and reliability, making it ideal for large-scale optimization tasks.
    

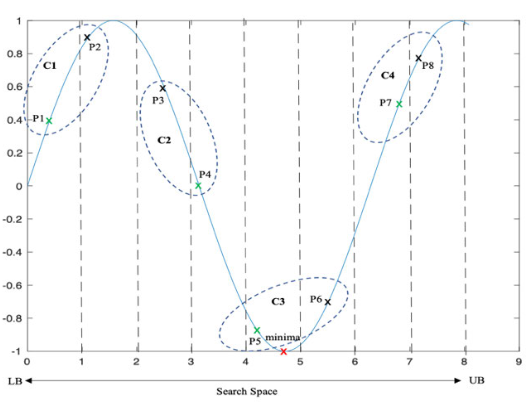
Illustration of the proposed experimental design.