Samir Brahim Belhaouari

Abstract. The nonlinear properties of chaos present promising approaches for enhancing cryptographic systems. This study introduces a novel chaos-based hash function leveraging the Collatz Conjecture, sine infinity, and chaos theory. The function, defined as: \(x_{n+1} = 10M \cdot \begin{cases} R_K (f(x_n) \sin(g(x_n)) + x_n) & \text{if } x_n \in (R - Z) \\ \left(\frac{x_n}{2^j}\right) \cdot P_{2j+1} & \text{if } \text{mod}(x_n, 2^j) = 0, 3 \leq j \leq 5 \\ \left(R(f(x_n)) \sin(g(x_n))\right) + x_n & \text{if } \text{mod}(x_n, 2^2) = 0 \\ \left(\frac{x_n}{2}\right) \cdot P_2 + 1 & \text{if } \text{mod}(x_n, 2) = 0 \\ x_n \cdot P_{\text{mod}(x_n, NP)} + 1 & \text{if } \text{mod}(x_n, 2) = 1 \end{cases}\)
enhances ergodicity and entropy, crucial for cryptographic applications. Performance evaluations indicate superior collision resistance and uniformity compared to SHA-2 and SHA-3. The proposed hash function achieves an average hamming distance of 50.33\% and exhibits robust security properties under various datasets and conditions.
    

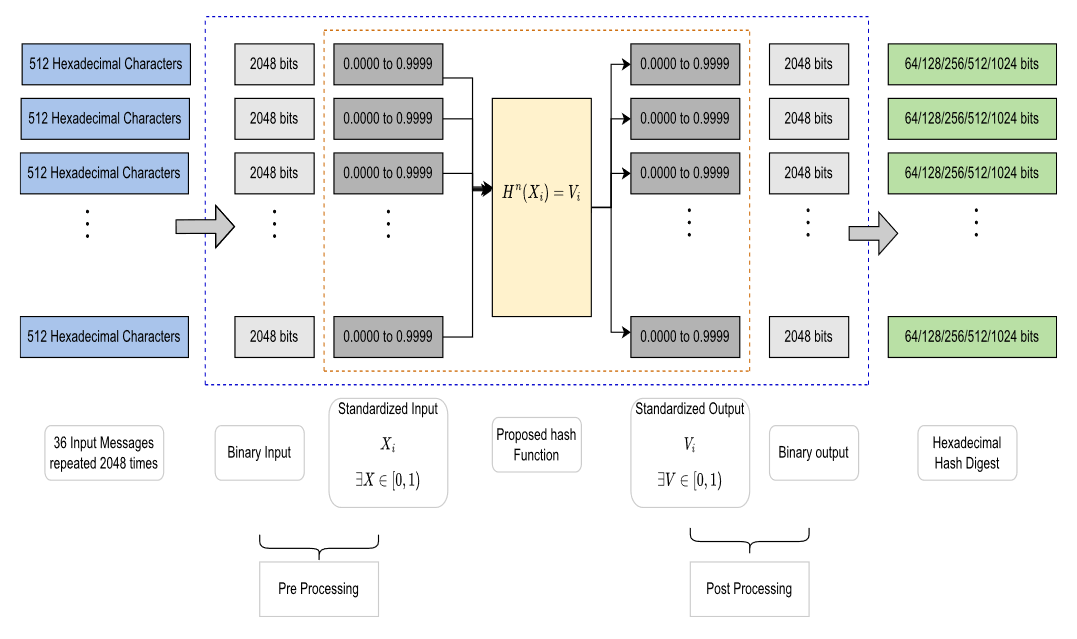
Illustration of the proposed experimental design.